§ 2.16. НОВЫЕ ИНТЕГРАЛЬНЫЕ СООТНОШЕНИЯ В ТЕОРИИ НЕСТАЦИОНАРНОГО ТЕПЛОПЕРЕНОСА НА ОСНОВЕ УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА

Классические задачи нестационарного теплопереноса, рассматриваемые в этой книге, основаны на уравнении энергии (2.1), которое можно записать в виде:

,  ,  .         (2.657)

Входящие в (2.657) вектор плотности теплового потока  имеет вид классической зависимости Фурье

,                            (2.658)

которая описывает распространение тепла диффузным способом. Соотношения (2.657) – (2.658) приводят к уравнению нестационарной теплопроводности параболического типа (2.1) и соответствующим краевым задачам (2.1) – (2.3). Аналитические решения этих задач показывают, что скорость распространения тепла в изучаемых средах является бесконечной. Для большинства практических задач нестационарной теплопроводности классическая феноменология Фурье (2.658) даёт удовлетворительные результаты. Более того: для уравнений параболического типа (2.1) краевые задачи (2.1) – (2.3) являются предметом практически необозримого числа исследований. С годами их поток не уменьшается, охватывая все новые содержательные математические объекты и все большее число самых разнообразных приложений, учитывая наличие хорошо разработанных аналитических методов, дающих точное решение задачи (2.1) – (2.3).

В последние десятилетия в аналитической теории теплопроводности (и родственных процессов) развивается направление, учитывающее конечную скорость распространения тепла при исследовании теплообмена с помощью модельных представлений на основе обобщённого закона теплопроводности . Для анизотропных тел этот закон установил С. Калиски , вводя в принцип Онзагера характеристику скорости изменения теплового потока – тепловую инерцию. Для изотропных тел закон, обобщающий (2.658), установил А.В. Лыков  как гипотезу о конечных скоростях распространения тепла и массы для тепло – и влагопереноса в капиллярно – пористых телах. Согласно

,                      (2.659)

где  - время релаксации теплового потока, связанное со скоростью распространения тепла  соотношением .  Для металлов ; для азота ; для аморфных тел типа неорганического стекла и полимеров, имеющих сложную структуру, время релаксации достигает значений ( - )с; опытное измерение  во многих случаях не представляется возможным. Скорость распространения тепла для стали , для алюминия , что превышает скорость распространения звука; для азота  и для газов в условиях разряжённого сверхзвукового потока влияние конечной скорости распространения тепла на теплообмен становится заметным. Подобное влияние может проявляться также при очень низких температурах (например, в жидком гелии  при ) и даже при обычных температурах в твёрдых телах, когда в нестационарном процессе рассматривается малый период времени .

Соотношения (2.657) и (2.659) приводят к уравнению теплопроводности гиперболического типа

,  , .                (2.660)

Можно выделить большой класс моделей, основанных на уравнении (2.660). Так, гиперболическое уравнение используется для описания температурных полей, возникающих при высокоинтенсивном теплообмене в устройствах импульсной и лазерной техники; при лазерной обработке металлов; в процессах плазменного напыления; в энергетических каналах ядерных реакторов, в псевдоожиженном слое; в дисперсных системах и зернистых материалах; в слоистых полупроводниковых структурах; при описании процесса электронной теплопроводности в высокотемпературной плазме; при математическом моделировании фронтовых процессов терморазложения; в кристаллах катализатора и при выращиваний гомоэпитаксиальных плёнок германия, возникающих в ходе экзотермических химических реакций и др. . Задачи теплопроводности на основе гиперболического уравнения (2.660) называются обобщёнными. С математической точки зрения, обобщённые задачи нестационарного переноса значительно отличаются от классических (2.1) – (2.3), являясь более сложными при нахождении аналитических решений.

Следует подчеркнуть, что достигнутые за последние два – три десятилетия успехи в нахождении точных аналитических решений краевых задач для уравнения (2.660) весьма незначительны. Последнее объясняется несовершенством математического аппарата, приспособленного для решения обобщённых задач, в частности, отсутствием в известных справочниках по операционному исчислению ( и др.) формул обращения для изображений, возникающих при решении гиперболического уравнения. В то же время найденные решения содержат неточности , как в самих  функциональных конструкциях аналитических решений, так и в исходной постановке задачи. Для уравнения (2.660) чаще используются классические граничные условия (2.3), а не интегральная форма записи этих условий, вытекающая из обобщённого закона (2.659). Ниже эти вопросы разбираются детальным образом. Формулируется также математический аппарат в виде интегральных соотношений, достаточно эффективных при нахождении точных аналитических решений тепловых задач обобщённого типа.

Рассмотрим сначала область ; этот случай наиболее часто всречается в приложениях и требует ряда уточнений. Уравнение (2.660) при отсутствии внутреннего  источника тепла (его наличие рассмотрим ниже) имеет вид:

,  ,  .               (2.661)

Рассмотрим уравнение (2.661) при постоянных начальных условиях:

,  ,  ,  .          (2.662)

Наличие постоянных или переменных (по координате) начальных условий в области  имеет принципиальное значение для записи обобщённых граничных условий для гиперболического уравнения.

Граничное условие 1 рода (температурный нагрев) записывается аналогично, как и для уравнения (2.1):

,   .                                 (2.663)

Граничное условие 2 рода (тепловой нагрев) при постоянных начальных условиях (2.662) на основании (2.659) имеет обобщённый интегральный вид:

,   .         (2.664)

Граничное условие 3 рода (нагрев средой) при начальных условиях (2.662) имеет также вид обобщённой интегральной формы записи:

,   .        (2.665)

К этим условиям необходимо добавить ещё одно граничное условие:

,   ,   .                              (2.666)

При формальном переходе (2.664) – (2.665) к дифференциальной форме записи граничных условий следует проявлять осторожность, так как в случае постоянных граничных функций , , ,  дифференциальная форма записи не будет эквивалентна интегральной (2.664) – (2.665) (не удовлетворяет (2.664) – (2.665)) и получаемые далее аналитические решения тепловой задачи не являются истинными. В действительности, дифференциальная форма обобщённых граничных условий 2 и 3 родов, эквивалентная интегральным условиям (2.664) – (2.665) имеет вид:

для условий (2.664)

,   ,                    (2.667)

если  - переменная величина и

,   ,                    (2.668)

если , где  - дельта – функция Дирака;

для условий (2.665)

,    ,          (2.669)

если  - переменная величина и

,     ,                (2.670)

если

Рассмотрим далее соотношения (2.661) – (2.666) в безразмерных переменных:

;    ;    ;   ;        (),

;           .                  (2.671)

Имеем:

,     ,     ;             (2.672)

,      ;               (2.673)

Граничные условия:

,     ;                              (2.674)

либо

,      ;              (2.675)

либо

,   ;(2.676)

,      ,      .                         (2.677)

В пространстве изображений по Лапласу

,                       (2.678)

решение уравнения (2.672) с учётом (2.677) сводится к выражениям вида , где вид зависимости  определяется типом граничного условия (2.674) – (2.676). Приведём ряд формул операционного исчисления, полученных для решения задач типа (2.672) – (2.677):

,                    (2.679)

где

,   ,                          (2.680)

 - импульсная функция,    - модифицированная функция Бесселя;

;                      (2.681)

;                               (2.682)

;             (2.683)

свёртка функций  и  есть

;                        (2.684)

свёртка функций  и

есть

.                               (2.685)

Теперь можно записать аналитические решения всех трёх краевых задач нестационарной теплопроводности, рассмотренных в (2.672) – (2.677).

Теперь можно записать аналитические решения всех трёх краевых задач нестационарной теплопроводности, рассмотренных в (2.672) – (2.677). Для уменьшения громоздкости в (2.674) – (2.676) достаточно рассмотреть случаи

,                                     (2.686)

учитывая, что общий случай несложно записать на основе приведённых выше соотношений. Имеем:

,                              (2.687)

где

В пространстве оригиналов находим:

,                                      (2.688)

где

,     ,                       (2.689)

Если в уравнении (2.672) присутствует функция источника тепла, то есть

,    ,            (2.690)

и краевые условия имеют вид (2.673) – (2.677), (2.686), то к правой части операционного решения (2.687) необходимо прибавить слагаемое

,                             (2.691)

где . Оригинал (2.691) находится по приведённым выше формулам обращения.

Приведённые рассуждения показывают, что нахождение аналитических решений задач теплопереноса для уравнений гиперболического типа даже для простейшей области ,  технически значительно труднее классических случаев (2.1) – (2.3). Другой особенностью полученных операционных решений является возможность представления для частично ограниченной области аналитического решения одной и той же задачи в различных классах функций, что не имеет место для задач (2.1) – (2.3) на основе феноменологии Фурье (для (2.1) – (2.3) такая возможность имеет место только в ограниченных областях канонического типа, когда аналитическое решение задачи имеет  вид ряда типа Фурье – Бесселя, либо формулы суммирования Пуассона ). Если в (2.687) переходить к оригиналам по формуле обращения с помощью контурного интеграла Римана - Меллина

,       (2.692)

и вычислять интеграл (2.692) непосредственно при наличии двух точек ветвления  и , то в отличие от (2.688) – (2.689) аналитические решения будут иметь следующий вид:

задача 1 (температурный нагрев (2.674), (2.686))

     (2.693)

задача 2 (тепловой нагрев (2.675), (2.686)

                                                (2.694)

задача 3 (нагрев средой (2.676), (2.686))

    (2.695)

Эти решения тождественны в смысле числа и, по-видимому, могут быть преобразованы друг в друга, что является достаточно сложной задачей вычислительной математики.

Рис. 2.5. Температурные кривые в сечении z¢ =2 при с₀ = 0,001:

——— - температурный нагрев (решение( 2.693));

‑‑‑‑‑‑‑‑‑ - тепловой нагрев (решение 2.694);

……… - нагрев средой при Bi = 5 (решение (2.695))

 

На рис. 2.5. приведены кривые изменения температуры от F_o в сечении  при с_o = 0,001,  построенные по формулам (2.693)-(2.695). Здесь, как и в классическом случае (2.1) - (2.3) существует пограничное значение , ниже которого температурный нагрев (задача 1) является наиболее интенсивным, причем с увеличением параметра с_o, величина смещается в сторону меньших значений. Этот факт был установлен в термомеханике при исследовании динамической реакции массивного тела на тепловой удар [87] в рамках моделей (2.1) - (2.3). Было показано, что среди различных (традиционных) видов теплового нагружения температурный нагрев является наиболее опасным режимом.

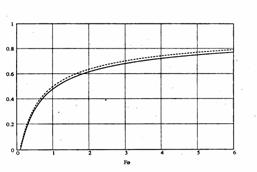
Рис. 2.6. Тепловая реакция области в сечении z¢ =2

 при температурном нагреве:

——— - решение( 2.688);

‑‑‑‑‑‑‑‑‑ - решение (2.693)

 

Рис. 2.6. описывает тепловую реакцию области в сечении  при с_o = 0,001 при температурном нагреве (задача 1), полученную по формулам (2.688) и (2.693). Некоторое различие кривых связано с особенностью вычислительных схем при численной обработке соотношений (2.688) и (2.693).

Рассмотрим далее метод функции Грина для краевых задач переноса гиперболического типа. Уравнение (2.660) запишем в виде

             (2.696)

где - известная функция.

Функция Грина  по переменным (M,t) удовлетворяет условиям:

               (2.697)

                                (2.698)

                     (2.699)

а по переменным

            (2.700)

                              (2.701)

 

                    (2.702)

Соотношения (2.697) - (2.702) имеют важное значение для последующих рассуждений. Рассмотрим равенство:

                      (2.703)

Равенство (2.703) проинтегрируем по  и преобразуем далее, используя формулу Грина для оператора Лапласа [75]. Получим

       (2.704)

Соотношение (2.704) справедливо при всех  и, следовательно, его можно проинтегрировать по τ для , где - сколь угодно малое число. Получим:

                       (2.705)

При подынтегральные функции слева в (2.705) достаточно регулярны, так как исключена особенность функции в точке  при . Меняем порядок интегрирования слева и вычисляем интегралы (по τ), используя (2.701), (2.702). Переходя к пределу при  с учетом соотношения  находим окончательно интегральное представление для аналитических решений через функцию влияния:

                            (2.706)

Используя соотношение (2.706), запишем интегральную форму аналитических решений для задач (2.672) – (2.677):

,                           (2.707)

где

,    ,      для первой краевой задачи;

,    ,      для второй краевой задачи;

,    ,      для первой краевой задачи;

Для случаев (2.668) и (2.670) выражение (2.707) имеет вид:

,        (2.708)

где

,    ,    ;

,    ,    ;

Функция Грина  находится из решения задачи:

,    ,      ;                   (2.709)

,     ,      ;                (2.710)

,      ;                     (2.711)

,     ,    ,                    (2.712)

где

,  для первой краевой задачи;

,  для второй краевой задачи;

,  для третьей краевой задачи.

В пространстве изображений (по Лапласу)

     ()         (2.713)

функция Грина как решение задачи (2.709) – (2.712) имеет вид:

      (2.714)

где

;                    ,       для  в (2.707);

,          для  в (2.707);

        для  в (2.707).

В ряде практических случаев можно уменьшить громоздкость в записи аналитических решений задач для уравнения (2.661) на основе анализа параметра , где  - скорость звука в материале, ; ,  - изотермические коэффициенты Ламе;  - плотность. В качестве иллюстрации рассмотрим (2.661) в конечной области ,  при начальных условиях (2.662), граничных условиях (2.663) и (2.665) соответственно га границах области  и  при ; . Перейдём к следующим безразмерным переменным;

;   ;   ;    ;

;    .                         (2.715)

Граничное условие (2.665) в переменных (2.715) будет иметь вид

,   .           (2.716)

Рассмотрим случай, когда , т.е. . Анализ условия (2.716) в пространстве изображений по Лапласу (2.678) при  показывает, что от (2.716) можно перейти к классическому условию теплообмена и, таким образом, исходная задача будет иметь вид:

,   ;  ;               (2.717)

,   ;                   (2.718)

,    ;                    (2.719)

,   .                                       (2.720)

Приведённые выше операционные соотношения приводят к решению задачи (2.717) – (2.720) в виде

,              (2.721)

;

;

 - полином Лагера; ; .

Сравнивая решение (2.721) с классическими для задачи (2.1) – (2.3) при  , можно ещё раз убедиться, что краевые задачи нестационарного переноса для уравнений гиперболического типа требуют пристального внимания в аналитической теории теплопроводности твёрдых тел. Дальнейшее обобщение гиперболической модели нестационарного переноса – переход к областям с движущимися  во времени границами. Подобные задачи возникают во многих направлениях науки и техники, описанных в  и аналитические методы для нахождения точных решений такого рода задач практически не разработаны. Возможно, более эффективными здесь окажутся приближённые аналитические методы, изложению которых посвящены следующие разделы книги.